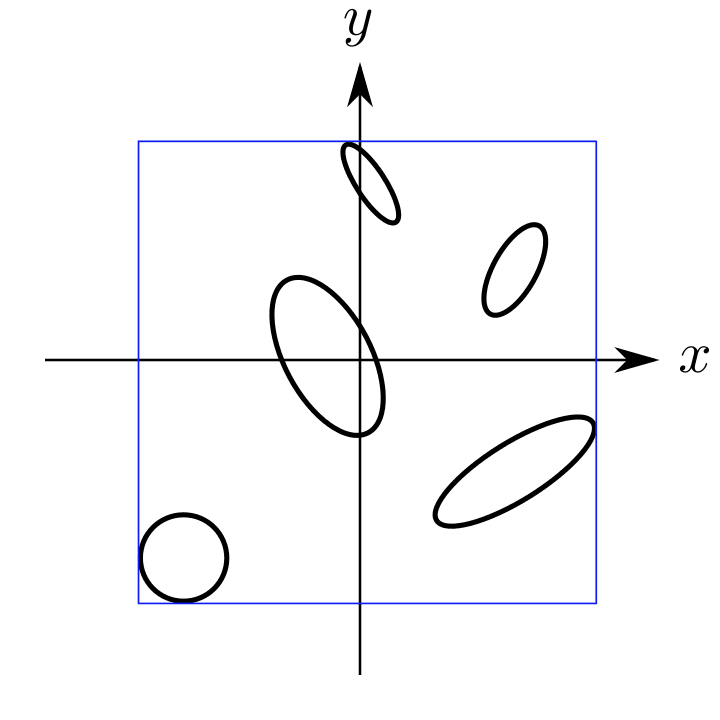
xy平面上に配置されている楕円に対し、これらの楕円を囲う長方形を求めたい。
長方形を導出する方法について教えて欲しい。
こんなお悩みを解決します。
今回の記事は、こちらのサイトで楕円と長方形の関係について考察されていたことが発端となります。
論理的な内容は検討されていましたが、実際のプログラムが記載されていなかったため、実装してみました。
楕円の存在する領域を求める方法や実装方法を知りたい方に向けて、解説しているのでぜひご覧ください。
効率良く技術習得したい方へ
短期間でプログラミング技術を習得したい場合は、経験者からフォローしてもらえる環境下で勉強することをおすすめします。
詳細は、以下の記事をご覧ください。
-

-
【比較】プログラミングスクールおすすめランキング6選【初心者向け】
続きを見る
数学的な背景
リンク先で以下のように問題設定が行われているため、この内容に従って整理します。
問題設定
今回は,有限個の楕円が平面状に散らばっている状況を考える.この状況において,すべての楕円を含む長方形領域の最小値を求める問題を解く. 図で示すと以下のような長方形領域を求めることになる.
楕円が存在する領域算出したい長方形(参考サイトをもとに作成)
領域の計算方法
リンク先のサイトをもとに、計算方法を整理します。
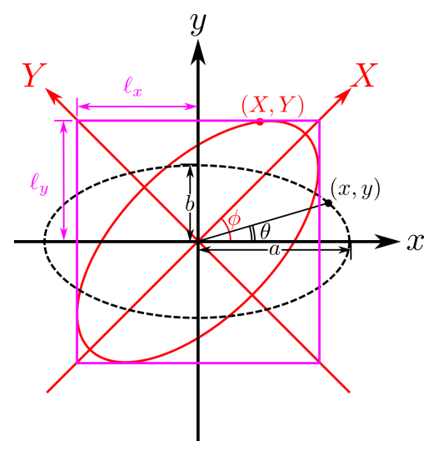
上記の図において、楕円の方程式は、以下のようになります。
$$
\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1
$$
ここで、\(a > 0, b > 0\)です。
また、楕円上の点\((x, y)\)は、媒介変数\(\theta\)を用いると以下のようになりますね。
$$
\left\{
\begin{array}{ccc}
x & = & a\cos{\theta} \\
y & = & b\sin{\theta} \\
\end{array}
\right.
$$
この時、楕円を\(\phi\)だけ回転させた場合の移動後の点\((X, Y)\)は、回転行列を用いると以下のように算出できます。
$$
\begin{eqnarray*}
\left(
\begin{array}{c}
X \\
Y \\
\end{array}
\right) & = & \left(
\begin{array}{cc}
\cos{\phi} & \sin{\phi} \\
-\sin{\phi} & \cos{\phi} \\
\end{array}
\right)\left(
\begin{array}{c}
x \\
y \\
\end{array}
\right) \\
& = & \left(
\begin{array}{cc}
\cos{\phi} & \sin{\phi} \\
-\sin{\phi} & \cos{\phi} \\
\end{array}
\right)\left(
\begin{array}{c}
a\cos{\theta} \\
b\sin{\theta} \\
\end{array}
\right) \\
& = & \left(
\begin{array}{c}
a\cos{\phi}\cos{\theta} + b\sin{\phi}\sin{\theta} \\
b\cos{\phi}\sin{\theta} - a\sin{\phi}\cos{\theta} \\
\end{array}
\right)
\end{eqnarray*}
$$
さらに、三角関数の合成を用いると上記の式は、以下のように表現できますね。
$$
\begin{eqnarray*}
X & = & \sqrt{a^{2} \cos^{2}{\phi} + b^{2}\sin^{2}{\phi}} \cos{(\theta - \gamma_{X})} \\
Y & = & \sqrt{b^{2} \cos^{2}{\phi} + a^{2}\sin^{2}{\phi}} \sin{(\theta - \gamma_{Y})}
\end{eqnarray*}
$$
ここで、\(\gamma_{X}, \gamma_{Y}\)は、それぞれ以下を満たします。
$$
\begin{eqnarray*}
\cos{\gamma_{X}} & = & \frac{a\cos{\phi}}{ \sqrt{a^{2} \cos^{2}{\phi} + b^{2}\sin^{2}{\phi}} } \\
\sin{\gamma_{X}} & = & \frac{b\sin{\phi}}{ \sqrt{a^{2} \cos^{2}{\phi} + b^{2}\sin^{2}{\phi}} } \\
\cos{\gamma_{Y}} & = & \frac{b\cos{\phi}}{ \sqrt{b^{2} \cos^{2}{\phi} + a^{2}\sin^{2}{\phi}} } \\
\sin{\gamma_{Y}} & = & \frac{a\sin{\phi}}{ \sqrt{b^{2} \cos^{2}{\phi} + a^{2}\sin^{2}{\phi}} }
\end{eqnarray*}
$$
よって、\(X, Y\)がそれぞれ最大となるときが求める長方形領域の半分の長さとなるため、\(\ell_{x}, \ell_{y}\)は、以下のようになります。
$$
\begin{eqnarray*}
\ell_{x} & = & \sqrt{a^{2} \cos^{2}{\phi} + b^{2}\sin^{2}{\phi}} \\
\ell_{y} & = & \sqrt{b^{2} \cos^{2}{\phi} + a^{2}\sin^{2}{\phi}}
\end{eqnarray*}
$$
上記までの内容は、参考サイト:楕円が存在する領域の内容に基づいて作成しています。
プログラムによる実装
今回のプログラムは、以下に格納しています。

また、求める領域は、以下の青色の領域とします。

実装時の考え方
青色の領域は、以下の方法で求めることができます。
- 各楕円に接する長方形の存在領域(ピンク色の破線部分)を算出する。
- 1.で求めた長方形のうち、最小・最大となる領域(青色の実線部分)を算出する。
以降では、C言語での実装例とPythonでの実装例を示します。
C言語の実装例
ファイル構成
./
|-- Makefile
|-- include/
| `-- searchMaxRectangle.h
|-- python/
| `-- search_max_rectangle.py
`-- src/
|-- searchMaxRectangle.c
`-- main.c
ヘッダー
#ifndef SEARCH_MAX_RECTANGLE_H_
#define SEARCH_MAX_RECTANGLE_H_
#define SMR_SUCCESS (0)
#define SMR_FAILED (1)
struct SMR_rectangle_t {
/**
*
* min_x max_x
* | |
* V V
* +---------------+ <- max_y
* | |
* | |
* | Rectangle |
* | |
* | |
* +---------------+ <- min_y
*
*/
double min_x;
double max_x;
double min_y;
double max_y;
};
struct SMR_ellipse_t {
double x0; /* x coordinate of center of ellipse */
double y0; /* y coordinate of center of ellipse */
double A; /* major axis */
double B; /* minor axis */
double phi; /* rotation angle [degree] */
};
/**
* @brief find the largest rectangle that encloses multiple ellipses
* @param[in] num number of ellipses
* @param[in] ellipses target ellipses
* @param[out] max_rectangle output rectangle
* @return SMR_SUCCESS success this process
* SMR_FAILED failed this process
*/
extern int search_max_rectangle(
int num,
const struct SMR_ellipse_t *ellipses,
struct SMR_rectangle_t *max_rectangle
);
#endif // SEARCH_MAX_RECTANGLE_H_ソースコード
#include <stddef.h>
#include <math.h>
#include "searchMaxRectangle.h"
#define SMR_RETURN_OK (0)
#define SMR_RETURN_NG (1)
#define SMR_MAX(a, b) (((a) > (b)) ? (a) : (b));
#define SMR_MIN(a, b) (((a) < (b)) ? (a) : (b));
/**
* @brief calculate rectangle size
* @param[in] ellipse target ellipse
* @param[out] rectangle output rectangle
* @return SMR_RETURN_OK success
* SMR_RETURN_NG failed
*/
static int calculate_rectangle_size(
const struct SMR_ellipse_t *ellipse,
struct SMR_rectangle_t *rectangle
);
int search_max_rectangle(
int num,
const struct SMR_ellipse_t *ellipses,
struct SMR_rectangle_t *max_rectangle
) {
int ret = (int)SMR_FAILED;
int func_val;
int idx;
const struct SMR_ellipse_t *current;
struct SMR_rectangle_t target;
if ((NULL != ellipses) && (NULL != max_rectangle)) {
current = &ellipses[0];
func_val = calculate_rectangle_size(current, max_rectangle);
if ((int)SMR_RETURN_OK != func_val) {
goto EXIT_SEARCH_MAX_RECTANGLE;
}
for (idx = 1; idx < num; idx++) {
current = &ellipses[idx];
func_val = calculate_rectangle_size(current, &target);
if ((int)SMR_RETURN_OK != func_val) {
goto EXIT_SEARCH_MAX_RECTANGLE;
}
/* swap if the ellipse is father away */
max_rectangle->min_x = SMR_MIN(target.min_x, max_rectangle->min_x);
max_rectangle->min_y = SMR_MIN(target.min_y, max_rectangle->min_y);
max_rectangle->max_x = SMR_MAX(target.max_x, max_rectangle->max_x);
max_rectangle->max_y = SMR_MAX(target.max_y, max_rectangle->max_y);
}
ret = (int)SMR_SUCCESS;
}
EXIT_SEARCH_MAX_RECTANGLE:
return ret;
}
static int calculate_rectangle_size(
const struct SMR_ellipse_t *ellipse,
struct SMR_rectangle_t *rectangle
) {
int ret = (int)SMR_RETURN_NG;
double x0, y0, phi;
double sq_major_axis, sq_minor_axis;
double sq_sin, sq_cos;
if ((NULL != ellipse) && (NULL != rectangle)) {
/* convert degrees to radians */
phi = ellipse->phi * M_PI / 180.0;
x0 = ellipse->x0;
y0 = ellipse->y0;
sq_major_axis = pow(ellipse->A, 2.0);
sq_minor_axis = pow(ellipse->B, 2.0);
sq_sin = pow(sin(phi), 2.0);
sq_cos = pow(cos(phi), 2.0);
/* calculate rectangle size */
rectangle->max_x = sqrt(sq_major_axis * sq_cos + sq_minor_axis * sq_sin);
rectangle->max_y = sqrt(sq_major_axis * sq_sin + sq_minor_axis * sq_cos);
rectangle->min_x = -rectangle->max_x;
rectangle->min_y = -rectangle->max_y;
/* translation */
rectangle->max_x += x0;
rectangle->max_y += y0;
rectangle->min_x += x0;
rectangle->min_y += y0;
ret = (int)SMR_RETURN_OK;
}
return ret;
}Python
import math
from dataclasses import dataclass
@dataclass
class Rectangle:
"""
min_x max_x
| |
V V
+---------------+ <- max_y
| |
| |
| Rectangle |
| |
| |
+---------------+ <- min_y
"""
min_x: float
min_y: float
max_x: float
max_y: float
@dataclass
class Ellipse:
x0: float # x coordinate of center of ellipse
y0: float # y coordinate of center of ellipse
A: float # major axis
B: float # minor axis
phi: float # rotation angle [degree]
class SearchMaxRectangle:
def calculate_rectangle_size(self, ellipse):
"""
Parameters
----------
ellipse : Ellipse
Returns
-------
rectangle : Rectangle
"""
# convert degrees to radians
phi = math.radians(ellipse.phi)
x0 = ellipse.x0;
y0 = ellipse.y0;
sq_major_axis = ellipse.A ** 2.0
sq_minor_axis = ellipse.B ** 2.0
sq_sin = math.sin(phi) ** 2.0
sq_cos = math.cos(phi) ** 2.0
# calculate rectangle size
ell_x = math.sqrt(sq_major_axis * sq_cos + sq_minor_axis * sq_sin);
ell_y = math.sqrt(sq_major_axis * sq_sin + sq_minor_axis * sq_cos);
# translate ellipse and create rectangle
rectangle = Rectangle(
min_x=-ell_x+x0, max_x=ell_x+x0,
min_y=-ell_y+y0, max_y=ell_y+y0,
)
return rectangle
def search(self, ellipses):
"""
Parameters
----------
ellipse : list of Ellipse
Returns
-------
max_rectangle : Rectangle
"""
rectangles = [
self.calculate_rectangle_size(ellipse)
for ellipse in ellipses
]
max_rectangle = Rectangle(
min_x=min(map(lambda rect: rect.min_x, rectangles)),
min_y=min(map(lambda rect: rect.min_y, rectangles)),
max_x=max(map(lambda rect: rect.max_x, rectangles)),
max_y=max(map(lambda rect: rect.max_y, rectangles)),
)
return max_rectangle実行例
今回は、以下に示す5つの楕円に対し、青色の領域を求めてみます。
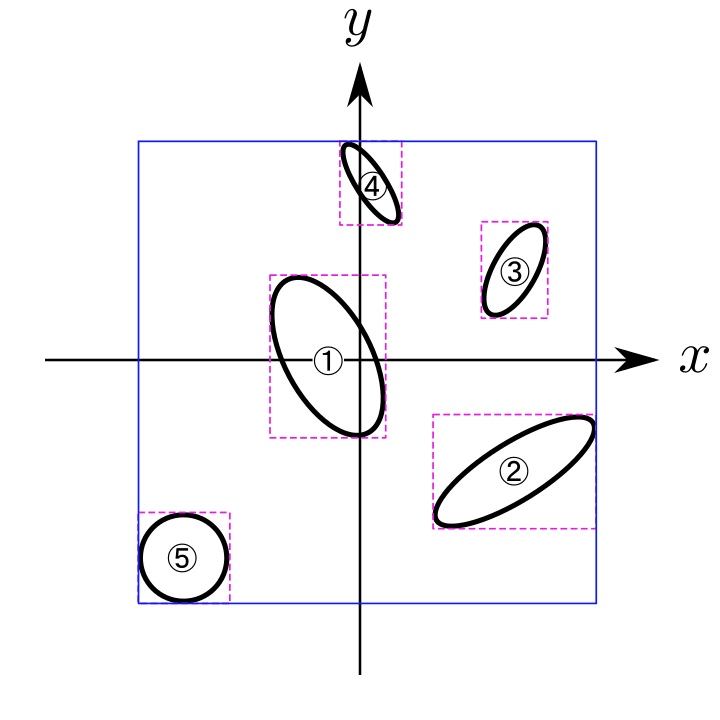
ここで、それぞれの楕円の式と回転角を以下のように定義します。
| 番号 | 楕円の式 | 回転角\(\phi[\textrm{degree}]\) |
|---|---|---|
| ① | \(\dfrac{(x + 3)^{2}}{6^{2}} + \dfrac{(y - 1)^{2}}{3^{2}} = 1\) | \(118^{\circ}\) |
| ② | \(\dfrac{(x - 10)^{2}}{6.4^{2}} + \dfrac{(y + 7)^{2}}{2^{2}} = 1\) | \(32^{\circ}\) |
| ③ | \(\dfrac{(x - 10)^{2}}{3.5^{2}} + \dfrac{(y - 7)^{2}}{1.5^{2}} = 1\) | \(61^{\circ}\) |
| ④ | \(\dfrac{x^{2}}{3.2^{2}} + (y - 13)^{2} = 1\) | \(123^{\circ}\) |
| ⑤ | \(\dfrac{(x + 13)^{2}}{3^{2}} + \dfrac{(y + 13)^{2}}{3^{2}} = 1\) | \(0^{\circ}\) |
対象の長方形の算出
上記の図において、関連する楕円だけを残し、説明用の座標の情報を追加すると以下のようになります。(④の図が少しズレています)
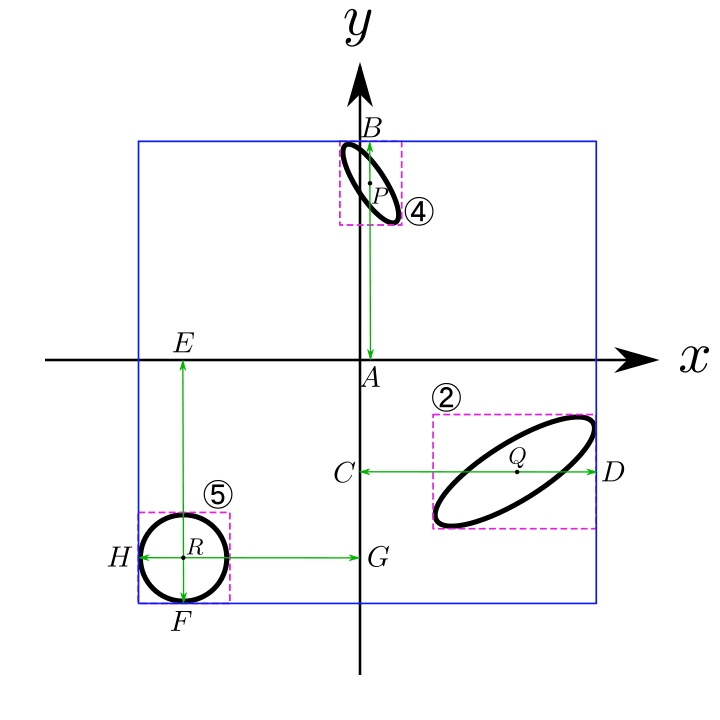
先程の導出結果を用いて関係する座標間の長さを算出すると、以下のようになりますね。
| 対象の線分 | 長さ |
|---|---|
| \(AB = AP + PB\) | \(13 + \sqrt{\cos{\left( \dfrac{123}{180}\pi \right)} + 3.2^{2}\sin{\left( \dfrac{123}{180}\pi \right)}} \approx 15.73845\) |
| \(CD = CQ + QD\) | \(10 + \sqrt{6.4^{2} \cos{\left( \dfrac{32}{180}\pi \right)} + 2^{2}\sin{\left( \dfrac{32}{180}\pi \right)}} \approx 15.53002\) |
| \(EF = ER + RF\) | \(GH = 13 + 3 = 16\) |
| \(GH = GR + RH\) | \(GH = 13 + 3 = 16\) |
プログラムによる求解
C言語では、以下のプログラムをコンパイルして実行することで、上記で算出した結果の符号付きの解を得られます。
#include <stdio.h>
#include "searchMaxRectangle.h"
#define MAX_ELLIPSE_NUM (5)
int main(void) {
int ret;
/* ellipse list */
struct SMR_ellipse_t ellipses[MAX_ELLIPSE_NUM] = {
{ -3.0, 1.0, 6.0, 3.0, 118.0},
{ 10.0, -7.0, 6.4, 2.0, 32.0},
{ 10.0, 7.0, 3.5, 1.5, 61.0},
{ 0.0, 13.0, 3.2, 1.0, 123.0},
{-13.0, -13.0, 3.0, 3.0, 0.0},
};
/* max rectangle */
struct SMR_rectangle_t max_rectangle;
/* search max rectangle */
ret = search_max_rectangle(
(int)MAX_ELLIPSE_NUM,
(const struct SMR_ellipse_t *)ellipses,
&max_rectangle
);
if ((int)SMR_SUCCESS != ret) {
goto EXIT_MAIN;
}
fprintf(stdout, "mininum coordinate x: %+.5lf\n", max_rectangle.min_x);
fprintf(stdout, "mininum coordinate y: %+.5lf\n", max_rectangle.min_y);
fprintf(stdout, "maxinum coordinate x: %+.5lf\n", max_rectangle.max_x);
fprintf(stdout, "maxinum coordinate y: %+.5lf\n", max_rectangle.max_y);
EXIT_MAIN:
return 0;
}また、Pythonでは、以下のスクリプトを実行することでC言語版と同様の解が得られます。
if __name__ == '__main__':
ellipses = [
Ellipse(x0=-3.0, y0=1.0, A=6.0, B=3.0, phi=118.0),
Ellipse(x0=10.0, y0=-7.0, A=6.4, B=2.0, phi=32.0),
Ellipse(x0=10.0, y0=7.0, A=3.5, B=1.5, phi=61.0),
Ellipse(x0=0.0, y0=13.0, A=3.2, B=1.0, phi=123.0),
Ellipse(x0=-13.0, y0=-13.0, A=3.0, B=3.0, phi=0.0),
]
smr = SearchMaxRectangle()
max_rectangle = smr.search(ellipses)
output = [
'mininum coordinate x: {:+.5f}'.format(max_rectangle.min_x),
'mininum coordinate y: {:+.5f}'.format(max_rectangle.min_y),
'maxinum coordinate x: {:+.5f}'.format(max_rectangle.max_x),
'maxinum coordinate y: {:+.5f}'.format(max_rectangle.max_y),
]
print('\n'.join(output))
まとめ
今回は、複数の楕円を囲う長方形の導出方法について解説しました。
解説した考え方を利用する機会は限定的ですが、数学的に導出した結果に基づいて実装する能力は、他の分野でも役立ちます。
類題を多く解くことで、導出結果をプログラムで実装する能力を身に付けてみてください。
効率良く技術習得したい方へ
今回の話の中で、プログラミングについてよく分からなかった方もいると思います。
このような場合、エラーが発生した際に対応できなくなってしまうため、経験者からフォローしてもらえる環境下で勉強することをおすすめします。
詳細は、以下の記事をご覧ください。
-

-
【比較】プログラミングスクールおすすめランキング6選【初心者向け】
続きを見る