【Pythonによる実装】部分ピボット選択付きガウスの消去法

悩んでいる人

普段ライブラリを利用しているが、原理的な部分の理解が曖昧なため、ガウスの消去法を自前で実装してみたい。

また、普段よく使う言語がPythonなため、Pythonによる実装例を知りたい。

こんなお悩みを解決します。

今回は、数値解析を実施する上で、一度は目にすることになる「ガウスの消去法」をPythonで実装したいと思います。

この記事では実装例のみを示すことになるため、ガウスの消去法の考え方に関しては、以下の記事を参考にしてください。

実装例

部分ピボット選択付きガウスの消去法の実装例は以下のようになります。

import numpy as np
def gaussian_elimination(_A, _b, pmeps=1e-10):
    """
    Parameters
    ----------
    _A : numpy.matrix
        coefficient matrix
    _b : numpy.ndarray
        right-hand side vector
    pmeps : double (option)
        pseudo machine epsilon
    Returns
    -------
    x : numpy.ndarray
        estimated vector
    """
    A = _A.copy()
    b = _b.copy()
    ndim = A.shape[-1]
    for idx in np.arange(ndim - 1):
        # search maximum value in idx-th column
        pos = np.abs(A[idx:, idx]).argmax()
        if pos != 0:
            # calculate the pivot
            pivot = pos + idx
            # swap
            A[idx, :], A[pivot, :] = A[pivot, :].copy(), A[idx, :].copy()
            b[idx], b[pivot] = b[pivot], b[idx]
        diag = A[idx, idx]
        if (np.abs(diag) < pmeps):
            raise Exception(f'Error: diagonal component is less than pseudo machine eps={pmeps}')
        # =============
        # forward erase
        # =============
        for row in np.arange(idx + 1, ndim):
            scale = A[row, idx] / diag
            A[row, idx:] -= scale * A[idx, idx:]
            b[row] -= scale * b[idx]
    # =================
    # back substitution
    # =================
    b[-1] /= A[-1, -1]
    for row in np.arange(ndim - 1)[::-1]:
        b[row] = (b[row] - np.dot(A[row, (row+1):], b[(row+1):])) / A[row, row]
    x = b.copy()
    return x

部分ピボット選択付きガウスの消去法の処理は、下記に示すように、3つに大別できます。

部分ピボット選択
前進消去（係数行列\(A\)を上三角行列に変形する）
後退代入

以降では、上記の順に、実装例と対比させながら解説します。

部分ピボット選択

ガウスの消去法では、前進消去時に行列の対角成分を利用して、上三角行列に近づけていきます。

その際に、対角成分で割る処理が入るのですが、対角成分の絶対値が0に近い値の場合、数値的に不安定になります。

これを極力回避するために、行を入れ替えるという作業をします。

これは、連立方程式の式自体を入れ替えていることと等価なため、解の順番には影響を与えません。

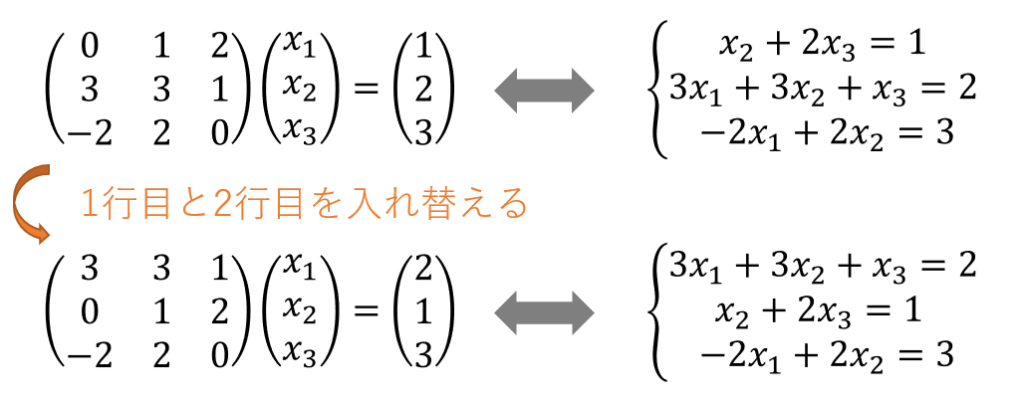
列のピボット選択を行うバージョンもありますが、変数の対応を覚えておく必要があるため、行のみを入れ替える部分ピボット選択が良く利用されます。

該当する実装は以下のようになります。

    for idx in np.arange(ndim - 1):
        # idx番目の対角成分以降の要素の中から、絶対値が最大となるインデックスを取得
        pos = np.abs(A[idx:, idx]).argmax()

        if pos != 0:
            # 係数行列の該当位置を算出（pivot）
            pivot = pos + idx
            # 行を入れ替える
            A[idx, :], A[pivot, :] = A[pivot, :].copy(), A[idx, :].copy()
            b[idx], b[pivot] = b[pivot], b[idx]

Pythonでは、s, t = t, sといった代入が可能なため、この表記を使って入れ替え処理を実現しています。

前進消去

この処理では、対象とする列の対角成分以降の要素が0になるように係数行列と右辺ベクトルを変形していきます。

該当する実装は以下のようになります。

    # In for loop (loop variable: idx, range: from 0 to ndim - 2)
        for row in np.arange(idx + 1, ndim):
            # 対角成分に対するスケール値を計算
            scale = A[row, idx] / diag
            # 対角成分以降の要素が0になるように係数行列を変形
            A[row, idx:] -= scale * A[idx, idx:]
            b[row] -= scale * b[idx]

後退代入

前進消去後、係数行列は上三角行列に変形できているため、行列の下から上に向かって解くことで、未知変数を求めることができます。

該当する実装は以下のようになります。

    b[-1] /= A[-1, -1]
    for row in np.arange(ndim - 1)[::-1]:
        b[row] = (b[row] - np.dot(A[row, (row+1):], b[(row+1):])) / A[row, row]

動作確認

動作確認用のスクリプトの例として、以下のようなものを用意しました。

# データ定義
ndim = 10
A = np.matrix(np.random.normal(3.1, 4.1, (ndim, ndim)), dtype=np.float64)
xexact = np.arange(ndim, dtype=np.float64) + 1 # 真値
b = np.ravel(A @ xexact) # 行列計算により右辺ベクトルを算出

# 未知数を推定
x = gaussian_elimination(A, b)
# 推定結果を出力
print('estimated: ', x)

これを実行すると以下のような結果が得られます。

estimated:  [ 1.  2.  3.  4.  5.  6.  7.  8.  9. 10.]

また、今回の実装例は以下で公開しています。使い方もあわせて掲載しているので、参考にしてください。

https://github.com/yuruto-free/gaussian-elimination-in-python

まとめ

今回は、ガウスの消去法をPythonで実装しました。

Pythonには数多くのライブラリが用意されているため、自前で実装する必要はほとんどないと思いますが、内容を理解するという観点では重要な取り組みになると思います。

少しでも興味を持った方は、実際に動かしてみたり、処理を追ってみてください。

【Pythonによる実装】部分ピボット選択付きガウスの消去法

【解説＆実装】ガウスの消去法

実装例

部分ピボット選択

前進消去

後退代入

動作確認

まとめ